- Research
- Open access
- Published:
Analytical properties of generalized Gaussian distributions
Journal of Statistical Distributions and Applications volume 5, Article number: 6 (2018)
Abstract
The family of Generalized Gaussian (GG) distributions has received considerable attention from the engineering community, due to the flexible parametric form of its probability density function, in modeling many physical phenomena. However, very little is known about the analytical properties of this family of distributions, and the aim of this work is to fill this gap.
Roughly, this work consists of four parts. The first part of the paper analyzes properties of moments, absolute moments, the Mellin transform, and the cumulative distribution function. For example, it is shown that the family of GG distributions has a natural order with respect to second-order stochastic dominance.
The second part of the paper studies product decompositions of GG random variables. In particular, it is shown that a GG random variable can be decomposed into a product of a GG random variable (of a different order) and an independent positive random variable. The properties of this decomposition are carefully examined.
The third part of the paper examines properties of the characteristic function of the GG distribution. For example, the distribution of the zeros of the characteristic function is analyzed. Moreover, asymptotically tight bounds on the characteristic function are derived that give an exact tail behavior of the characteristic function. Finally, a complete characterization of conditions under which GG random variables are infinitely divisible and self-decomposable is given.
The fourth part of the paper concludes this work by summarizing a number of important open questions.
Introduction
The goal of this work is to study a large family of probability distributions, termed Generalized Gaussian (GG), that has received considerable attention in many engineering applications. We shall refer to Xp with the GG distribution given by the probability density function (pdf)
as \(X_{p}\sim \mathcal {N}_{p} \left (\mu,\alpha ^{p}\right)\), and where we define the gamma function, the lower incomplete gamma function and the upper incomplete gamma function as
respectively. Another commonly used name for this type of distribution, especially in economics, is the Generalized Error distribution. The flexible parametric form of the pdf of the GG distribution allows for tails that are either heavier than Gaussian (p<2) or lighter than Gaussian (p>2) which makes it an excellent choice for many modeling scenarios. The origin of the GG family can be traced to the seminal work of Subbotin (1923) and Lévy (1925). In fact, Subbotin (1923) has shown that the same axioms used by Gauss (1809) to derive the normal distribution, are also satisfied by the GG distribution. Well-known examples of this distribution include: the Laplace distribution for p=1; the Gaussian distribution for p=2; and the uniform distribution on [μ−α,μ+α] for p=∞.
1.1 Past work
The GG distribution has found use in image processing applications where many statistical features of an image are naturally modeled by distributions that are heavier-tailed than Gaussian.
For example, Gabor coefficients are convolution kernels whose frequency and orientation representations are similar to those of the human visual system. Gabor coefficients have found a wide range of applications in texture retrieval and face-recognition problems. However, a considerable drawback of using Gabor coefficients is the memory requirements needed to store a Gabor representation of an image. In Gonzalez-Jimenez et al. (2007) GG distributions with the parameter p<2 have been shown to accurately approximate the empirical distribution of Gabor coefficients in terms of the Kullback-Liebler (KL) divergence and the χ2 distance. Moreover, the authors in (Gonzalez-Jimenez et al. 2007) demonstrated that data compression algorithms based on the GG statistical model considerably reduce the memory required to store Gabor coefficients.
In a classical image retrieval problem, a system searches for K images similar to a query image from a digital library containing a total of N images (usually K≪N). In (Do and Vetterli 2002) by modeling wavelet coefficients with a GG distribution and using the KL divergence as a similarity measure, the authors were able to improve retrieval rates by 65% to 70%, compared with traditional approaches.
Other applications of the GG distribution in image processing applications include modeling: textured images, see Mallat (1989); Moulin and Liu (1999) and de Wouwer et al. (1999); pixels forming fine-resolution synthetic aperture radar (SAR) images (Bernard et al. 2006); and the distribution of values in subband decompositions of video signals Westerink et al. (1991) and Sharifi and Leon-Garcia (1995).
In communication theory, the GG distribution finds many modeling applications in impulsive noise channels which occur when the noise pdf has a longer tail than the Gaussian pdf. For example, in Beaulieu and Young (2009) it is shown that in ultrawideband (UWB) systems with time-hopping (TH) the interference should be modeled with probability distributions that are more impulsive than the Gaussian. Moreover, it has been shown that for the moderate and high signal-to-noise ratio (SNR) the interference in the TH-UWB is well modeled by the GG distribution with a parameter p≤1. In Algazi and Lerner (1964) and Miller and Thomas (1972) certain atmospheric noises were shown to be impulsive and GG distributions with parameter values of 0.1<p<0.6 were shown to provide good approximations to their distributions.
GG distributions can also model noise distributions that appear in non-standard wireless media. In Nielsen and B.Thomas (1987) the authors showed that Arctic under-ice noise is well modeled by members of the GG family. In Banerjee and Agrawal (2013) the GG family has been recognized as a model for the underwater acoustic channel where values of p=2.2 and p=1.6 have been found to model the ship transit noise and the sea surface agitation noise, respectively.
The problem of designing optimal detectors for signals in the presence of GG noise has been considered in Miller and Thomas (1972); Poor and Thomas (1978) and Viswanathan and Ansari (1989). In Soury et al. (2012) the authors studied the average bit error probability of binary coherent signaling over flat fading channels subject to additive GG noise. Interestingly, the authors of Soury et al. (2012) give an exact expression for the average probability of error in terms of Fox’s H functions.
In power systems, the GG distribution has been used to model hourly peak load model demand in power grids (Mohamed et al. 2008).
In Varanasi and Aazhang (1989) the authors studied a problem of estimating parameters of the GG distribution (order p, mean μ, and variance \(\sigma ^{2}=\mathbb {E}\left [(X_{p}-\mu)^{2}\right ]\)) from n independent realizations of a GG random variable. The authors of (Varanasi and Aazhang 1989) considered three estimation methods, namely, the method of moments, maximum likelihood, and moment/Newton-step estimators, and compared performance of each for different values of p. For example, in the vicinity of p=2, the moment method was shown to perform best. In (Richter 2007) the authors established connections between chi-square and Student’s t-distribution. Moreover, in Richter (2016), using the notions of generalized chi-square and Fisher statistics introduced in Richter (2007), the authors studied a problem of inferring one or two scaling parameters of the GG distribution and derived both the confidence interval and significance test.
The Shannon capacity of channels with GG noise has been considered in Fahs and Abou-Faycal (2018) and Dytso et al. (2017b). In Fahs and Abou-Faycal (2018) the authors gave general results on the structure of the optimal input distribution in channels with GG noise under a large family of channel input cost constraints. In Dytso et al. (2017b) the authors investigated the capacity of channels with GG noise under Lp moment constraints and proposed several upper and lower bounds that are asymptotically tight.
As the pdf of GG distributions has a very simple form, many quantities such as moments, entropy, and Rényi entropy can be easily computed (Do and Vetterli 2002; Nadarajah 2005). Also, from the information theoretic perspective the GG distribution is interesting because it maximizes the entropy under a p-th absolute moment constraint (Cover and Thomas 2006; Lutwak et al. 2007). The maximum entropy property can serve as an important intermediate step in a number of proofs. For example, in (Dytso et al. 2018) it has been used to generalize the Ozarow-Wyner bound (Ozarow and Wyner 1990) on the mutual information of discrete inputs over arbitrary channels. In Nielsen and Nock (2017) the maximum entropy principle has been used to improve bounds on the entropy of Gaussian mixtures.
While the number of applications of the GG distribution is large, many of its properties have been drawn from numerical studies, and few analytical properties of the GG family are known beyond the cases p=1,2 and p=∞. For instance, very little is known about the characteristic function of the GG distribution and only expressions in terms of hypergeometric functions are known. For example, the characteristic function of the GG distribution was given in terms of Fox-Write functions in Pogány and Nadarajah (2010) for all p>1 and later generalized in terms of Fox-H functions in Soury and Alouini (2015) for all p>0. The work of Soury and Alouini (2015), also characterized the pdf of the sum of two independent GG random variables in terms of Fox-H functions. Specific non-linear transformations of sums of independent GG distributions and the moment generating function of the GG distribution have been studied in Vasudevay and Kumari (2013).
There is also a large body of work on multivariate GG distributions. For example, to the best of our knowledge, the first multivariate generalization was introduced in (De Simoni 1968) where the exponent was taken to be \( \left (\left (\textbf {x}- \boldsymbol {\mu }\right)^{T} \textbf {K}^{-1} (\textbf {x}-\boldsymbol {\mu }) \right)^{\frac {p}{2}}\) where x and μ are vectors and K is a matrix. In Goodman and Kotz (1973) the authors introduced yet another multivariate generalization of the GG distribution in (1): X is said to be multivariate GG if and only if it can be written as X=KZ+μ where the components of Z are independently and identically distributed according to the univariate GG distribution in (1). An example of multivariate distributions with GG marginals and examples of multivariate GG distributions defined with respect to other norms the interested reader is referred to Richter (2014); Arellano-Valle and Richter (2012) and Gupta and Nagar (2018) and the references therein.
1.2 Paper outline and contributions
Our contributions are as follows:
-
1
In “Moments and the Mellin transform” section, we study properties of the moments of the GG distribution including the following:
-
In Proposition 1 we derive an expression for the Mellin transform of the GG distribution; and
-
In Proposition 2 we show necessary and sufficient conditions under which moments of the GG distribution uniquely determine the distribution.
-
-
2
In “Properties of the distribution” section, we study properties of the distribution including the following:
-
In “Stochastic ordering” section, Proposition 3 shows that the family of GG distributions is an ordered set where the order is taken in terms of second-order stochastic dominance; and
-
In “Relation to completely monotone functions and positive definiteness” section, Theorem 1 connects the pdf of GG distributions to positive definite functions. In particular, we show that for p≤2 the pdf of the GG distribution is a positive definite function and for p>2 the pdf is not a positive definite function. Moreover, it is shown that for p≤2 the pdf of the GG distribution can be expressed as an integral of a Gaussian pdf with respect to a non-negative finite Borel measure.
-
-
3
In “On product decomposition of GG random variables” section, Proposition 5 shows that the GG random variable Xp can be decomposed into a product of two independent random variables Xp=V·Xr where Xr is a GG random variable. We carefully study properties of this decomposition including the following:
-
In “On the PDF of Vp,q” section, Proposition 6 gives power series and integral representations of the pdf of V; and
-
In “On the determinacy of the distribution of VG,q” section, Proposition 8 shows under which conditions the distribution of V is completely determined by its moments. Interestingly, the range for values of p for which Xp and V are determinant is not the same. This gives an interesting example that the product of two determinate random variables is not necessarily determinate.
-
-
4
In “Characteristic function” section, we study properties of the characteristic function of the GG distribution including the following:
-
In “Connection to stable distributions” section, Proposition 9 discusses connections between a class of GG distributions and a class of symmetric stable distributions;
-
In “Analyticity of the characteristic function” section, Proposition 10 shows under what conditions the characteristic function of the GG distribution is a real analytic function;
-
In “On the distribution of zeros of the characteristic function” section, Theorem 3 studies the distribution of zeros of the characteristic function of the GG distribution. In particular, it is shown that for p≤2 the characteristic function of the GG distribution has no zeros and is always positive, and for p>2 the characteristic function has at least one positive-to-negative zero crossing; and
-
In “Asymptotic behavior of ϕp(t)” section, Proposition 11 gives the tail behavior of the characteristic function of the GG distribution and its derivatives. The consequences of this result are discussed.
-
-
5
In “Additive decomposition of a GG random variable” section, we study additive decompositions of the GG random variables including the following:
-
In “Infinite divisibility of the characteristic function” section, Theorem 5 completely characterizes for which values of p the GG random variable is infinitely divisible. In addition, Proposition 14 studies properties of the canonical Lévy-Khinchine representation of infinitely divisible distributions; and
-
In “Self-decomposability of the characteristic function” section, Theorem 6 characterizes conditions under which a GG distribution of order p can be additively transformed into another GG distribution of order q. In the case of p=q this corresponds to answering if a GG distribution is self-decomposable.
-
The paper is concluded in “Discussion and conclusion” section by reflecting on future directions.
1.3 Other parametrization of the PDF
In addition to the parametrization used in (1), there are several other parametrization used in the literature. For example, Subbotin in his seminal paper (Subbotin 1923) used the following parametrization, which is still a commonly used notation amongst probability theorists:
In some engineering literature where variance models power it is convenient to work with the distributions where the variance is taken to be independent of the parameter p (e.g., (Gonzalez-Jimenez et al. 2007) and Miller and Thomas (1972))
In statistical literature, some authors prefer to use (e.g., (Richter 2016))
In the above parametrization the p-th moment, when μ=0, is normalized such that it equals to σp.
The choice of the parametrization is usually dictated by the application that one has in mind. In this work, we choose to work with the parametrization in (1) which we found to be convenient for studying the Mellin transform and the characteristic function of the GG distribution.
Moments and the Mellin transform
In this section, we study properties of the moments, absolute moments and Mellin transform of the GG distribution. We also show conditions under which the moments of Xp uniquely characterize its distribution. While the majority of the results in this section are not new or are easy to derive, we choose to include them for completeness as most of the development in other section will heavily depend on properties of moments.
2.1 Moments, absolute moments, and the Mellin transform
Definition 1
(Mellin Transform (Poularikas 1998).) The Mellin transform of a positive random variable X is defined as
The Mellin transform emerges as a major tool in characterizing products of positive independent random variables since
Proposition 1
(Mellin Transform of |Xp|.) For any p>0 and \(X_{p} \sim \mathcal {N}_{p} (0, \alpha ^{p})\)
Moreover, for any p>0 and k>−1 the absolute moments are given by
Proof
The Mellin transform can be computed by using the integral (Poularikas 1998, Table 8.1)
and, therefore,
where in the last step we used the value of cp in (1). Moreover, the above integral is finite if Re(s)>0 and p>0. The proof of (11) follows by choosing s=k+1 in (10). This concludes the proof. □
Note that the p-th absolute moment of Xp is given by \(\mathbb {E}\left [\left |X_{p}\right |^{p}\right ]= \frac {2\alpha ^{p}}{p}.\)
The expression in (11) can also be extended to multivariate GG distributions defined through ℓp norms; see for example Lutwak et al. (2007) and Arellano-Valle and Richter (2012).
The following corollary, which relates k-th moments of two GG distributions of a different order, is useful in many proofs.
Corollary 1
Let \(X_{q} \sim \mathcal {N}_{q}(0,1)\) and \(X_{p} \sim \mathcal {N}_{p}(0,1)\). Then, for q≥p>0
for any \(k \in \mathbb {R}^{+}\). Moreover, for q>p
Proof
See Appendix A. □
2.2 Moment problem
The classical moment problem asks whether a distribution can be uniquely determined by its moments. For random variables defined on \(\mathbb {R}\), this problem goes under the name of the Hamburger moment problem and for random variables on \(\mathbb {R}^{+}\) under the name of the Stieltjes moment problem (Stoyanov 2000). If the answer is affirmative, we say that the moment problem is determinate. Otherwise, we say that the moment problem is indeterminate and there exists another distribution that shares the same moments.
Proposition 2
The GG distribution is determinate for p∈[1,∞) and indeterminate for p∈(0,1).
Proof
We first show that for p∈(0,1) the GG distribution is indeterminate. To show that an absolutely continuous distribution with a pdf f(x) is indeterminate it is enough to check the classical Krein sufficient condition (Stoyanov 2000) given by
In other words, if (15) is satisfied, then the distribution is indeterminate. For the GG distribution, the condition in (15) reduces to showing
which is finite if p∈(0,1). Therefore, for p∈(0,1) the GG distribution is indeterminate.
To show that the distribution is determinate it is enough to show that the characteristic function has a power series expansion with a positive radius of convergence. For the GG distribution with p∈[1,∞), this will be done in Proposition 10. □
The interested reader is referred to [Lin and Huang (1997), Theorem 2] and [Hoffman-Jørgensen (2017), p. 301] where the conditions for the moment determinacy are provided for a Double Generalized Gamma distribution of which a GG distribution is special case.
Remark 1
To show that for p∈(0,1) there are distributions with the same moments as GG distributions, one can modify the example in [Stoyanov (2000), Chapter 11.4]. Specifically, for any ε∈(0,1) there exists ρ,r and λ such that the pdf
has the same integer moments as a GG distribution.
Remark 2
In (Varanasi and Aazhang 1989) the authors studied the problem of estimating the parameter p from n independent realizations of a GG random variable. As one of the proposed methods, the authors used empirical moments to estimate the parameter p. Moreover, in Varanasi and Aazhang (1989) it has been observed that the method of moments performs poorly for p∈(0,1). In view of Proposition 2, the observation about the method of moments made in Varanasi and Aazhang (1989) can be attributed to the fact that the GG distribution is indeterminate for p∈(0,1).
Properties of the distribution
3.1 Stochastic ordering
The cumulative distribution function (CDF) of \(X_{p}~\sim \mathcal {N}_{p}(\mu, \alpha ^{p})\) is given by
Corollary 1 suggests that there might be some ordering between members of the GG family. To make this point more explicit we need the following definition.
Definition 2
A random variable X dominates another random variable Y in the sense of the first-order stochastic dominance if
A random variable X dominates another random variable Y in the sense of the second-order stochastic dominance if
Proposition 3
Let \(X_{p}\sim \mathcal {N}_{p}(0,1)\) and \(X_{q}\sim \mathcal {N}_{q}(0,1)\). Then, for p≤q, Xq dominates Xp in the sense of the second-order stochastic dominance.
Proof
See Appendix B. □
It can be shown that the first-order stochastic dominance does not hold since for p≤q
From Proposition 3 we have the following inequality for the expected value of functions of GG distributions.
Proposition 4
Let \(X_{q} \sim \mathcal {N}_{q}(0,1)\) and \(X_{p} \sim \mathcal {N}_{p}(0,1)\). Then, for p≤q and for any nondecreasing and concave function \(g: \mathbb {R} \to \mathbb {R}\) we have that
Proof
The inequality in (19) is equivalent to the second-order stochastic dominance. For more details, the interested reader is referred toLevy (1992). □
Examples of functions that satisfy the hypothesis of Proposition 4 are \(g(x)= x- \sqrt {x^{2}+1} \) and g(x)=−e−tx,t≥0. These choices lead to the following inequalities for p≤q:
In particular, the inequality in (21) shows that the Laplace transform of \(f_{X_{p}}\) (which exists if 1<p,q) is larger than the Laplace transform of \(f_{X_{q}}\).
3.2 Relation to completely monotone functions and positive definiteness
We begin by introducing the notion of completely monotone and Bernstein functions.
Definition 3
A function f:[0,∞)→[0,∞) is said to be completely monotone if
A function f:[0,∞)→[0,∞) is said to be a Bernstein function if the derivative of f is a completely monotone function.
Applying the well-known result fromSchilling et al. (2012), that the composition of a completely monotone function and a Bernstein function is completely monotone, on the function e−x (completely monotone) and the function \(\frac {x^{p}}{2}\) (Bernstein for p∈(0,1]) we obtain the following.
Corollary 2
For p∈(0,1] the function \( \mathrm {e}^{-\frac {x^{p}}{ 2 }}\) is completely monotone.
For p>1 the function \(\mathrm {e}^{-x^{p}}\) is not completely monotone.
As will be observed throughout this paper, the GG distribution exhibits different properties depending on whether p≤2 or p>2. At the heart of this behavior is the concept of positive-definite functions.
Definition 4
(Positive Definite Function (Stewart 1976).) A function \(f: \mathbb {R} \to \mathbb {C}\) is called positive definite if for every positive integer n and all real numbers x1,x2,...,xn, the n×n matrix
is positive semi-definite.
The next result relates the pdf of the GG distribution to the class of positive definite functions.
Theorem 1
The function \( \mathrm {e}^{-\frac {| x|^{p}}{ 2 }}\) is
-
not positive definite for p∈(2,∞); and
-
positive definite for p∈(0,2]. Moreover, there exists a finite non-negative Borel measure μp on \(\mathbb {R}^{+}\) such that for x>0
$$ \mathrm{e}^{-\frac{x^{p}}{2}}= \int_{0}^{\infty} e^{-\frac{t}{2}x^{2}} d\mu_{p}(t). $$(24)
Proof
See Appendix C. □
The expression in (24) will form a basis for much of the analysis in the regime p∈(0,2] and will play an important role in examining properties of the characteristic function of the GG distribution. The following corollary of Theorem 1 will also be useful.
Corollary 3
For any 0<q≤p≤2 let \(r= \frac {2q}{p}\). Then, for x>0
Proof
The proof follows by substituting x in (24) with \(x^{\frac {q}{p}}\). □
On product decomposition of GG random variables
As a consequence of Theorem 1 we have the following decompositional representation of the GG random variable.
Proposition 5
For any 0<q≤p≤2 let \(X_{q} \sim \mathcal {N}_{q}(0,1)\). Then,
where Vp,q is a positive random variable independent of \( X_{\frac {2q}{p}} \sim \mathcal {N}_{\frac {2q}{p}}(0,1)\), and where =d denotes equality in distribution. Moreover, Vp,q has the following properties:
-
Vp,q is an unbounded random variable for p<2 and Vp,q=1 for p=2; and
-
for p<2, Vp,q is a continuous random variable with pdf given by
$$ f_{V_{p,q}}(v)= \frac{1}{2\pi} \frac{\Gamma \left(\frac{p}{2q} \right)}{\Gamma \left(\frac{1}{q} \right)} \int_{\mathbb{R}} v^{-it-1} \frac{2^{\frac{it}{q}} \Gamma \left(\frac{it +1}{q}\right)}{2^{\frac{itp}{2q}} \Gamma \left(\frac{p(it+1)}{2q}\right)} dt, \; v>0. $$(26b)
Proof
See Appendix D. □
Proposition 5 can be used to show that the GG random distribution is a Gaussian mixture which is formally defined next.
Definition 5
A random variable X is called a (centered) Gaussian mixture if there exists a positive random variable V and a standard Gaussian random variable Z, independent of V, such that X=dVZ.
As a consequence of Proposition 5 we have the following result.
Corollary 4
For q∈(0,2], \(X_{q}\sim \mathcal {N}_{q}(0,1)\) is a Gaussian mixture. In other words,
where Vq,q is independent of X2 and its pdf is defined in (26b).
Proof
The proof follows by choosing p=q in (26a). □
Another case of importance is
where X1 is a Laplace random variable. For the ease of notation the special cases of Gaussian and Laplace mixtures will be denoted as follows in the sequel:
respectively.
4.1 On the PDF of V p,q
The expression for the pdf of Vp,q in (26b) can be difficult to analyze due to the complex nature of the integrand. The next result provides two new representations of the pdf of Vp,q that in many cases are easier to analyze than the expression in (26b).
Proposition 6
For 0<q≤p≤2 the pdf of a random variable Vp,q has the following representations:
-
1
Power Series Representation
$$ f_{V_{p,q}}(v)= \frac{ \Gamma \left(\frac{p}{2q} \right)}{ \Gamma \left(\frac{1}{q} \right)} \sum\limits_{k=1}^{\infty} a_{k} v^{kq}, \ v>0, $$(28)where
$$ a_{k}= \frac{q}{\pi} \frac{(-1)^{k+1} 2^{(kq+1) \left(\frac{p}{2q} -\frac{1}{q} \right)} \Gamma\left(\frac{kq}{2} +1 \right) \sin \left(\frac{\pi kq}{2} \right) }{k! }. $$(29) -
2
Integral Representation
$$ f_{V_{p,q}}(v)=\frac{q 2^{\frac{p}{2q}-\frac{1}{q}} \Gamma \left(\frac{p}{2q} \right)}{ \pi \Gamma \left(\frac{1}{q} \right)} \int_{0}^{\infty} \sin \left(a_{p} v^{q} x^{\frac{p}{2}} \right) \mathrm{e}^{-b_{p} v^{q} x^{\frac{p}{2}}-x} dx, $$(30)where
$$ a_{p}=2^{\frac{p}{2}-1} \sin \left(\frac{\pi p}{2} \right), b_{p}=2^{\frac{p}{2}-1} \cos \left(\frac{\pi p}{2} \right). $$(31)
Proof
See Appendix E. □
Remark 3
From (30) in Proposition 6, for the case of p=q=1 it is not difficult to see that the random variable VG,1 is distributed according to the Rayleigh distribution, since
The pdf of the random variable VG,q is plotted in Fig. 1. Interestingly, the slope of \(f_{V_{G,q}}(v)\) around v=0+ behaves very differently depending on whether q<1 or q>1. This behavior can be best illustrated by looking at the pdf of \(V_{G,q}^{2}\), that is \(f_{V_{G,q}^{2}}(v)= \frac {1}{2 \sqrt {v}} f_{V_{G,q}}\left (\sqrt {v}\right)\).
Proposition 7
Let \(f_{V_{G,q}^{2}}(v)\)be the pdf of the random variable \(V_{G,q}^{2}\). Then,
Proof
By using the power series expansion of \(f_{V_{G,q}}(v)\) in (28) and the transformation \(f_{V_{G,q}^{2}}(v)= \frac {1}{2 \sqrt {v}} f_{V_{G,q}}\left (\sqrt {v}\right)\) (recall VG,q is a non-negative random variable) we have that
The proof follows by taking the limit as v→0 in (34). □
As we will demonstrate later, the behavior of the pdf of VG,q around zero will be important in studying the asymptotic behavior of the characteristic function of Xq. This is reminiscent of the initial value theorem of the Laplace transform where the value of a function at zero can be used to estimate the asymptotic behavior of its Laplace transform. Indeed, as we will see, the characteristic function of Xq and the Laplace transform of \(V_{G,q}^{2}\) have a clear connection.
4.2 On the determinacy of the distribution of V G,q
Similar to the investigation in “Moment problem” section of whether GG distributions are determinant (uniquely determined by their moments) or not, we now conduct a similar investigation of the distributions of VG,q.
Proposition 8
The distribution of VG,q is determinant for \(q\ge \frac {2}{5}\).
Proof
To show that the distribution of VG,q is determinant we can use Carleman’s sufficient condition for positive random variables (Stoyanov 2000). This condition states that the distribution of VG,q is determinant if
Next using the expression for the k-th moment of VG,q given in Appendix D and the approximation of the ratio of moments shown in Appendix A we have that
Using the approximation in (36) in the sum in (35) we have that
By using conditions for the convergence of p-series the sum in (37) diverges if \( \frac {1}{2} \left (\frac {1}{q}-\frac {1}{2} \right) \ge 1\) or \(q \ge \frac {2}{5}\). Therefore, Carleman’s condition is satisfied if \(q \ge \frac {2}{5}\), and thus VG,q has a determinant distribution for \(q \ge \frac {2}{5}\). This concludes the proof. □
Remark 4
According to Proposition 2 and 8, for the range of values \(q \in \left [\frac {2}{5}, 1\right ]\) the random variable Xq=dVG,q·X2 is a product of two random variables with determinant distributions while Xq itself has an indeterminate distribution on \(q \in \left [\frac {2}{5}, 1\right ]\) by Proposition 2. This observation generates an interesting example illustrating that the product of two independent random variables with determinant distributions can have an indeterminate distribution.
Characteristic function
The focus of this section is on the characteristic function of the GG distribution. The characteristic function of the GG distribution can be written in the following integral forms.
Theorem 2
The characteristic function of \(X_{p} \sim \mathcal {N}_{p} (0,1)\) is given by
-
For any p>0
$$ \phi_{p}(t) = 2c_{p} \int_{0}^{\infty} \cos(t x) e^{-\frac{x^{p}}{2}} dx, \, t \in \mathbb{R}. $$(38a) -
For any p∈(0,2]
$$ \phi_{p}(t) = \mathbb{E} \left[ \mathrm{e}^{-\frac{t^{2} V_{G,p}^{2}}{2}} \right], \, t \in \mathbb{R}, $$(38b)where the density of a variable VG,p is defined in Proposition 5.
Proof
The proof of (38a) follows from the fact that \(e^{-\frac {|x|^{p}}{2} }\) is an even function which implies that the Fourier transform is equivalent to the cosine transform.
To show (38b) observe that
where the equalities follow from: a) the decomposition property in Proposition 5; and b) the independence of VG,p and X2 and the fact that the characteristic function of X2 is \(\mathrm {e}^{-\frac {t^{2}}{2}}\). This concludes the proof. □
As a consequence of the positive definiteness, ϕp(t), for p∈(0,2], has a more manageable form given in (38b). However, for p>2 it does not appear that ϕp(t) can be written in a more amenable form and the best simplification one can perform is a trivial symmetrization that converts the Fourier transform into the cosine transform in (38a). Nonetheless, the cosine representation in (38a) does allow us to simplify the implementation of the numerical calculation of ϕp(t). Examples of characteristic functions of \(X_{p} \sim \mathcal {N}_{p} (0,1)\) for several values of p are given in Fig. 2.
The following result is immediate by Theorem 2.
Corollary 5
For p∈(0,2], ϕp(t) is a decreasing function for t>0.
5.1 Connection to stable distributions
A class of distributions that is closed under convolution of independent copies is called stable. A more precise definition is given next.
Definition 6
Let X1 and X2 be independent copies of a random variable X. Then X is said to be stable if for all constants a>0 and b>0, there exist c>0 and d∈R such that
The defining relationship in (39) is equivalent to
where ϕX(t) is a characteristic function of a random variable X.
Throughout this work we will use stable distribution, stable random variable, and stable characteristic function interchangeably.
The characteristic function of a stable distribution has the following canonical representation:
where \(\mu \in \mathbb {R}\) is the shift-parameter, \(c \in \mathbb {R}^{+}\) is the scaling parameter, β∈[−1,1] is the skewness parameter, and α∈(0,2] is the order parameter. We refer the interested reader to (Zolotarev 1986) for a comprehensive treatment of the subject of stable distributions.
In this work we are interested in symmetric stable distributions (i.e., β=0) which also go under the name of α-stable distributions with the characteristic function given by
Observe that there is a duality between a class of symmetric stable distributions and a class of GG distributions with p∈(0,2]. Up to a normalizing constant, the pdf of a GG random variable is equal to the characteristic function of an α-stable random variable. Equivalently, the pdf of an α-stable random variable is equal, up to a normalizing constant, to the characteristic function of a GG random variable.
We exploit this duality to give, yet another, integral representation of the characteristic function of the GG distribution with parameter p∈(0,2].
Proposition 9
For p∈(0,2]∖{1}
where
Moreover, let the integrand in (43a) be given by
then:
-
Up(x) is a non-negative function;
-
For p∈(0,1), Up(x) is an increasing function with
$${\lim}_{x \to 0^{+}} U_{p}(x)=0, \, {\lim}_{x \to 1^{-}} U_{p}(x)=\infty; $$ -
For p∈(1,2], Up(x) is a decreasing function with
$${\lim}_{x \to 0^{+}} U_{p}(x)=\infty, \, {\lim}_{x \to 1^{-}} U_{p}(x)=0; $$ -
For all p∈(0,2]∖{1}
$${\lim}_{x \to 0^{+} }g_{p}(x)=0, \, {\lim}_{x \to 1^{-}} g_{p}(x)=0; \text{ and} $$ -
The function gp has a single maximum given by
$$\max_{x \in [0,1]} g_{p}(x)= \frac{1}{ \mathrm{e} |t|^{\frac{p}{p-1} }}. $$
Proof
The characterization in (43a) can be found in (Zolotarev 1986, Theorem 2.2.3). The proof of the properties of Up(x) is presented in Appendix F. □
Since the integral in Proposition 9 is performed over a finite interval, the characterization in Proposition 9 is especially useful for numerical computations of ϕp(t). The plots in Fig. 2, for p∈(0,2), are done by using the expression for ϕp(t) in (43a). To the best of our knowledge, the properties of Up(x) and gp(x), derived in Proposition 9, are new and facilitate a more efficient numerical computation of the integral representation of ϕp(t). The plot of the function Up(x) for p=0.5 and p=1.5 is shown in Fig. 3.
We suspect that most of the properties of ϕp(t) for p∈(0,2) that we derive in this paper can be found by using the integral expression in (43a). However, instead of taking this route we use the product decomposition in Proposition 5 to derive all the properties of ϕp(t). We believe that using a product decomposition is a more natural approach. Moreover, the positive random variables in Gaussian mixtures, VG,p in our case, naturally appear in a number of applications (e.g., bounds on the entropy of sum of independent random variables (Eskenazis et al. 2016)) and are of independent interest.
5.2 Analyticity of the characteristic function
An important question, in particular for numerical methods, is: when can the characteristic function of a random variable be represented as a power series of the form
The above expression is especially useful since the moments of GG distributions are known for every k; see Proposition 1.
Proposition 10
ϕp(t) is a real analytic function for
-
\(t \in \mathbb {R}\) for p>1; and
-
\( |t| < \frac {1}{2} \) for p=1.
For p<1 the function ϕp(t) is not real analytic.
Proof
See Appendix G. □
The results of Proposition 10 also lead to the conclusion that for p>1 the moment generating function of Xp, \(M_{p}(t)=\mathbb {E}\left [e^{{tX}_{p}}\right ]\) exists for all \(t\in \mathbb {R}\).
5.3 On the distribution of zeros of the characteristic function
As seen from Fig. 2 the characteristic function of the GG distribution can have zeros. The next theorem gives a somewhat surprising result on the distribution of zeros of ϕp(t).
Theorem 3
The characteristic function of ϕp(t) has the following properties:
-
for p>2, ϕp(t) has at least one positive to negative zero crossing. Moreover, the number of zeros is at most countable; and
-
for p∈(0,2], ϕp(t) is a positive function.
Proof
See Appendix H. □
Also, we conjecture that zeros of ϕp(t) have the following additional property.
Conjecture 1
For p∈(2,∞) zeros of ϕp(t) do not appear periodically.
It is important to point out that, for p=∞, the characteristic function is given by \(\phi _{\infty }(t)= \frac {\sin (t)}{t}=\text {sinc}(t)\), and zeros do appear periodically. However, for p<∞ we conjecture that zeros do not appear periodically.
5.4 Asymptotic behavior of ϕ p(t)
Next, we find the asymptotic behavior of ϕp(t) as t→∞. In fact, the next result gives the asymptotic behavior not only of \(\phi _{p}(t)=\mathbb {E} \left [ \mathrm {e}^{-\frac {V_{G,p}^{2} t^{2}}{2}} \right ]\) but also of a more general function
for some m>0. The analysis of the function in (45) also allows one to find asymptotic behavior on higher order derivatives of ϕp(t). For example, the first order derivative can be related to the function in (45) as follows:
Proposition 11
Let \(m \in \mathbb {R}^{+}\); then
Proof
See Appendix I. □
Using Proposition 11, we can give an exact tail behavior for ϕp(t).
Proposition 12
For p∈(0,2)
where A0 is defined in (46). Moreover, for 0<q,p<2 and some α>0
Proof
The proof follows immediately from Proposition 11. □
Note that, for p∈(0,2], the function \(\phi _{p}(\sqrt {2t})\) can be thought of as a Laplace transform of the pdf of the random variable \(V_{G,p}^{2}\). This observation together with the asymptotic behavior of ϕp(t) leads to the following result.
Proposition 13
For \(n\in \mathbb {R}\), \(\mathbb {E}[V_{G,p}^{n}]\) is finite if and only if n+p>−1.
Proof
For n>−1 the proof is a consequence of the decomposition property in Propositions 5 and 1 where it is shown that \(\mathbb {E}[|X_{p}|^{n}]<\infty \) if n>−1 for all p>0. Therefore, we assume that n<−1.
First observe that for any positive random variable X and k>0 the negative moments of X can be expressed as follows:
where F(t) is the Laplace transform of the pdf of X. Using the identity in (48) and the fact that \(\phi _{p}(\sqrt {2t})\) is the Laplace transform of the pdf of the random variable \(V_{G,p}^{2}\) we have that
Note that the integral in (49) is finite if and only if \( \phi _{p}\left (\sqrt {2t}\right) t^{k-1}= O \left (t^{-(1+\epsilon)}\right)\) for every ε>0. Moreover, by Proposition 12 we have that \(\phi _{p}\left (\sqrt {2t}\right) t^{k-1}= O \left (\frac {t^{k-1}}{t^{\frac {p+1}{2}}} \right)\), which implies that the integral in (49) is finite if and only if 2k−p<1. Setting 2k=−n concludes the proof. □
According to Proposition 1 and Proposition 5, for n>−1
while for n≤−1 it is not clear whether \(\mathbb {E}\left [V_{G,p}^{n}\right ]\) is finite since both moments \(\mathbb {E}[|X_{p}|^{n}]~=~\infty \) and \(\mathbb {E}[|X_{2}|^{n}]=\infty \). The result in Proposition 13 is interesting because it states that \(\mathbb {E}[V_{G,p}^{n}]\) is finite even if absolute moments of Xp and X2 are infinite. The result in Proposition 13 plays an important role in deriving non-Shannon type bounds in problems of communicating over channels with GG noise; see (Dytso et al. 2017b) for further details.
Additive decomposition of a GG random variable
In this section we are interested in determining whether a GG random variable \(X_{q}~\sim ~\mathcal {N}_{q}(0,\alpha ^{q})\) can be decomposed into a sum of two or more independent random variables.
6.1 Infinite divisibility of the characteristic function
Definition 7
A characteristic function ϕ(t) is said to be infinitely divisible if for every \(n \in \mathbb {N}\) there exists a characteristic function ϕn(t) such that
Similarly to stable distributions, we use infinitely divisible distribution, infinitely divisible random variable, and infinitely divisible characteristic function interchangeably.
Next we summarize properties of infinitely divisible distributions needed for our purposes.
Theorem 4
(Properties of Infinitely Divisible Distributions.) An infinitely divisible distribution satisfies the following properties:
-
1
((Lukacs 1970, Theorem 5.3.1).) An infinitely divisible characteristic function has no real zeros;
-
2
((van Harn and Steutel 2003, Theorem 10.1).) A symmetric distribution that has a completely monotone pdf on (0,∞) is infinitely divisible;
-
3
(Lévy-Khinchine canonical representation (Lukacs 1970, Theorem 5.5.1).) The function ϕ(t) is an infinitely divisible characteristic function if and only if it can be written as
$$ \log \left(\phi(t) \right)= ita + \int_{-\infty}^{\infty} \left(\mathrm{e}^{itx}-1 -\frac{itx}{1+x^{2}} \right) \frac{1+x^{2}}{x^{2}}d\theta(x), $$(51)where a is real and where θ(x) is a non-decreasing and bounded function such that \({\lim }_{x \to -\infty } \theta (x)=0\). The function dθ(x) is called the Lévy measure. The integrand is defined for x=0 by continuity to be equal to \(-\frac {t^{2}}{2}\). The representation in (51) is unique; and
-
4
((van Harn and Steutel 2003, Corollary 9.9).) A non-degenerate infinitely divisible random variable X has a Gaussian distribution if and only if it satisfies
$$ \limsup_{x \rightarrow \infty} \frac{- \log \mathbb{P}[ |X| \ge x] }{x \, \log (x)}=\infty. $$(52)
In general, the Lévy measure dθ is not a probability measure and hence the distribution function θ(x) is not bounded by one.
We use Theorem 4 to give a complete characterization of the infinite divisibility property of the GG distribution.
Theorem 5
A characteristic function ϕp(t) is infinitely divisible if and only if p∈ (0,1] ∪{2}.
Proof
For the regime p∈(0,1] in Corollary 2 it has been shown that the pdf is completely monotone on (0,∞). Therefore, by property 2) in Theorem 4 it follows that ϕp(t) is infinitely divisible for p∈(0,1].
Next observe that
where the equalities follow from: a) the expression for the CDF in (16); and b) using the limit \({\lim }_{x \to \infty } \frac {\Gamma (s,x)}{x^{s-1} \mathrm {e}^{-x} }=1\) (Olver 1991).
From the limit in (53) and since the distribution is Gaussian only for p=2 we have from property 4) in Theorem 4 that ϕp(t) is not infinitely divisible for p≥1 unless p=2.
Another proof that ϕp(t) is not infinitely divisible for p>2 follows from Theorem 3 since ϕp(t) has at least one zero, which violates property 1) of Theorem 4. This concludes the proof. □
Next, we show that the Lévy measure in the canonical representation in (51) is an absolutely continuous measure. This also allows us to give a new representation of ϕp(t) for p∈(0,1] where it is infinitely divisible.
Proposition 14
For p∈(0,1], the Lévy measure is absolutely continuous with density fθ(x) and ϕp(t) can be expressed as follows:
Moreover, for x≠0
Proof
See Appendix J. □
Remark 5
For the Laplace distribution with \(\phi _{1}(t)= \frac {1}{1+4t^{2}}\), the density fθ(x) can be computed by using (54b) and is given by
and the exponent in the Lévy-Khinchine representation is given by
6.2 Self-decomposability of the characteristic function
In this section we are interested in determining whether a GG random variable \(X_{q} \sim \mathcal {N}_{q}(0,\alpha ^{q})\) can be decomposed into a sum of two independent random variables in which one of the random variables is GG. Distributions with such a property are known as self-decomposable.
Definition 8
(Self-Decomposable Characteristic Function (Lukacs 1970;van Harn and Steutel 2003).) A characteristic function ϕ(t) is said to be self-decomposable if for every α≥1 there exists a characteristic function ψα(t) such that
In our context, the GG random variable \(X_{p} \sim \mathcal {N}_{p}(0,1)\) is self-decomposable if for every α≥1 there exists a random variable \(\hat {X}_{\alpha }\) such that
where \(Z_{p}\sim \mathcal {N}_{p}(0,1)\) is independent of \( \hat {X}_{\alpha }\).
In this section, we will look at a generalization of self-decomposability (in Eqs. (56) and (57)) and study whether there exists a random variable \(\hat {X}_{\alpha }\) independent of \(Z_{p} \sim \mathcal {N}_{p}(0,1)\) such that
where \(X_{q} \sim \mathcal {N}_{q}(0,1)\) for every α≥1. The decomposition in (58) finds application in information theory where the existence of the decomposition in (58) guarantees the achievability of Shannon’s bound on the capacity; see (Dytso et al. 2017b) for further details.
The existence of a random variable \( \hat {X}_{\alpha }\) is equivalent to showing that the function
is a valid characteristic function.
Observe that both Gaussian and Laplace are self-decomposable random variables. Self-decomposability of Gaussian random variables is a well known property. To see that the Laplace distribution is self-decomposable notice that
The expression in (60) is a convex combination of the characteristic function of a point mass at zero and the characteristic function of a Laplace distribution. Therefore, the expression in (60) is a characteristic function.
Checking whether a given function is a valid characteristic function is a notoriously difficult question, as it requires checking whether ϕ(q,p,α)(t) is a positive definite function; see (Ushakov 1999) for an in-depth discussion on this topic. However, a partial answer to this question can be given.
Theorem 6
For \((p,q) \in \mathbb {R}_{+}^{2}\) let
Then the function ϕ(q,p,α)(t) in (59) has the following properties:
-
for \((p,q) \in \mathbb {S}_{2}\), ϕ(q,p,α)(t) is a characteristic function (i.e., Xp is self-decomposable for p∈(0,1]∪{2});
-
for \((p,q) \in \mathbb {R}^{2}_{+} \setminus \mathbb {S}\), ϕ(q,p,α)(t) is not a characteristic function for any α≥1; and
-
for \( (p,q) \in \mathbb {S}_{1}\) and almost allFootnote 1 α≥1, ϕ(q,p,α)(t) is not a characteristic function.
Proof
See Appendix K. □
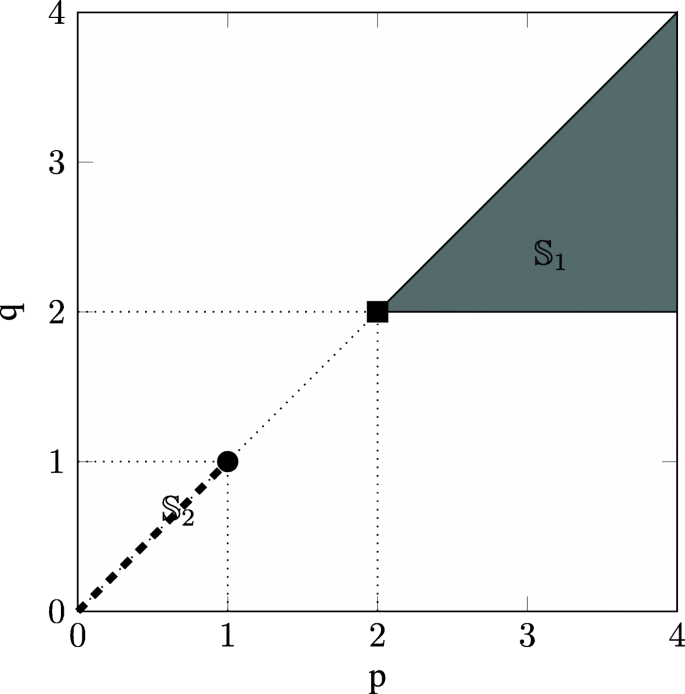
The result of Theorem 6 is depicted in Fig. 4
In the regime \(\mathbb {S}_{2}=\{(p,q): 0< p=q<1 \}\) (the dashed line) ϕ(q,p,α)(t) is self-decomposable. We also emphasize the point (p,q)=(2,2) (the black square) corresponds to the Gaussian characteristic function, and the point (p,q)=(1,1) (the black circle) corresponds to the Laplace characteristic function. The regime \(\mathbb {S}_{1}=\{ (q,p): 2< q < p \}\) (the gray triangle) is where ϕ(q,p,α)(t) is not a characteristic function for almost all α≥1. The white space is the regime where ϕ(q,p,α)(t) is not a characteristic function for all α≥1
We would like to point out that for 2<q≤p there are cases when ϕ(q,p,α)(t) is a characteristic function for some but not all α≥1. Specifically, let p=q=∞ in which case \(\phi _{\infty }(t)= \frac {\sin (t)}{t}=\text {sinc}(t)\) and
For example, when α=2 we have that \(\phi _{(\infty,\infty,\alpha)}(t)=\frac {1}{2} \cos (2t)\), which corresponds to the characteristic function of the random variable \(\hat {X}=\pm 1\) equally likely. Note that in the above example, because zeros of ϕp(t) occur periodically, we can select α such that the poles and zeros of ϕ(q,p,α)(t) cancel. However, we conjecture that such examples are only possible for p=∞, and for 2<p<∞ zeros of ϕp(t) do not appear periodically (see Conjecture 1) leading to the following:
Conjecture 2
For 2<q≤p<∞, ϕ(q,p,α)(t) is not a characteristic function for all α>1.
It is not difficult to check, by using the property that convolution with an analytic function is again analytic, that Conjecture 2 is true if p is an even integer and q is any non-even real number.
Discussion and conclusion
In this work we have focused on characterizing properties of the GG distribution. We have shown that for p∈(0,2] the GG random variable can be decomposed into a product of two independent random variables where the first random variable is a positive random variable and the second random variable is also a GG random variable. This decomposition was studied by providing several expressions for the pdf of the positive random variable.
A related open question is whether Proposition 5 can be extended to the regime of p>2. That is, the question is, can Xp be decomposed as follows:
for some positive random variable V independent of \(X_{q}\sim \mathcal {N}_{q}(0,1)\)? Noting that |X|p=dV ·|Xq| and using the Mellin transform method (recall that the Mellin transform works only for non-negative random variables) this question reduces to determining whether
is a proper characteristic function. A partial answer to this question is given next.
Proposition 15
The function ϕlog(V)(t)
-
for p>q, is not a valid characteristic function. Therefore, the decomposition in (62) does not exist; and
-
for p<q, is an integrable function. Moreover, if ϕlog(V)(t) is a valid characteristic function then the pdf of V is given by
$$ f_{V}(v)= \frac{1}{2 \pi} \frac{\Gamma \left(\frac{1}{q} \right)}{\Gamma \left(\frac{1}{p} \right)} \int_{\mathbb{R}} v^{-it-1} \frac{ 2^{\frac{it}{p}} \Gamma \left(\frac{it +1}{p}\right) }{ 2^{\frac{it}{q}} \Gamma \left(\frac{it +1}{q}\right)} dt, \ v>0. $$(63)
Proof
See Appendix L. □
To check if the decomposition in (62) exists for p<q one needs to verify whether the function in (63) is a valid pdf. Because of the complex nature of the integral it is not obvious whether the function in (63) is a valid pdf, and we leave this for future work.
We have also characterized several properties of the characteristic function of the GG distribution such as analyticity, the distribution of zeros, infinite divisibility and self-decomposability. Moreover, in the regime p∈(0,2) by exploiting the product decomposition we were able to give an exact behavior of the tail of the characteristic function.
We expect that the properties derived in this paper will be useful for a large audience of researchers. For example, in (Dytso et al.2017b,2018) we have used the result in this paper to answer important information theoretic questions about optimal communication over channels with GG noise and optimal compression of GG sources. In view of the fact that GG distributions maximize entropy under Lp moment constraints, we also expect that GG distributions will start to play an important role in finding bounds on the entropy of sums of random variables; see for example (Eskenazis et al. 2016) and (Dytso et al. 2017a) where GG distributions are used to derive such bounds.
Appendix A: Proof of Corollary 1
To show that \( \mathbb {E}\left [|X_{q}|^{k}\right ] \le \mathbb {E}\left [|X_{p}|^{k}\right ] \) for 0<p≤q let
The goal is to show that for every fixed k>0 the function gk(p) is decreasing in p. This result can be extracted from the next lemma which demonstrates a slightly more general result.
Lemma 1
Let
and let γdenote the Euler’s constant where γ≈0.57721. Then, for every fixed k>0 and log(a)>γ the function gk,a(x) is increasing in x>0.
Proof
Instead of working with gk,a(x) it is simpler to work with a logarithm of gk,a(x) (recall that logarithms preserve monotonicity)
Taking the derivative of fk,a(x) we have that
where ψ0(x) is the digamma function. Next using the series representation of the digamma function (Abramowitz and Stegun 1964) given by
we have that the derivative is given by
Clearly the terms in the summation in (68) are positive under the assumptions of the lemma and, hence, \(\frac {d}{dx} f_{k,a}(x) > 0\). This concludes the proof. □
Observing that \(g_{k}(p)= g_{k,2} \left (\frac {1}{p} \right)\) and log(2)≈0.693>γ≈0.577 concludes the proof that gk(p) is a decreasing function.
The second part follows by using Stiriling’s approximation \(\Gamma (x+1) \approx \sqrt { 2 \pi x} \left (\frac {x}{\mathrm {e}} \right)^{x}\) and the property that Γ(x+1)=xΓ(x) as follows:
The proof is concluded by taking the limit as k→∞ and using that q>p.
Appendix B: Proof of Proposition 3
The proof follows from the inequality:
for p≤q. For completeness the inequality in (69) is shown in Appendix B.1.
Without loss of generality assume that x>0 and observe that
where (71) follows from the symmetry and (72) follows from the inequality in (69). This concludes the proof.
B.1 Proof of the inequality in (69)
Let
The goal is to show that f(p,x) is an increasing function of p. To that end, observe that by using a change of variable \(u= (2t)^{\frac {1}{p}} \) the function f(p,x) can be written as
Therefore, showing monotonicity of f(p,x) is equivalent to showing that for p≤q
The inequality in (75) can be conveniently re-written as
and then the inequality in (76) follows by the monotonicity of the exponential function. This concludes the proof.
Appendix C: Proof of Theorem 1
To show that \( \mathrm {e}^{-\frac {| x|^{p}}{ 2 }}\) is not a positive definite function for p>2 it is enough to consider the following counterexample. In Definition 4 let n=3 and choose |x1−x2|=ε,|x2−x3|=aε and |x1−x3|=(a+1)ε for some ε,a>0. Therefore, the determinant of the matrix A is given by
The idea of the proof is to show that for a small ε we have that h(ε)<0. To that end, we use the following small t approximation \(\mathrm {e}^{t}= 1+t+\frac {t^{2}}{2}+O(t^{3})\) in (77)
The proof is concluded by taking ε small enough and noting that \( \frac { \left (\left (a+1\right)^{p}+a^{p}+1 \right)^{2}}{2} -a^{2p}- \left (a+1\right)^{2p}-1 \ge 0\) for p≤2 and \( \frac { \left (\left (a+1\right)^{p}+a^{p}+1 \right)^{2}}{2} -a^{2p}- \left (a+1\right)^{2p}-1 <0\) for p>2.
An easy way of see that \( \mathrm {e}^{-\frac {| x|^{p}}{ 2 }}\) is a positive definite function is by observing that \( \mathrm {e}^{-\frac {| x|^{p}}{ 2 }}\), for p∈(0,2], is a characteristic function of a stable distribution of order p. The proof then follows by Bochner’s theorem (Ushakov 1999, Theorem 1.3.1.) which guarantees that all characteristic functions are positive definite. For other proofs that \( \mathrm {e}^{-\frac {| x|^{p}}{ 2 }}\) is positive definite for p∈(0,2] we refer the reader to (Lévy 1925) and (Bochner 1937).
To show that \( \mathrm {e}^{-\frac {| x|^{p}}{ 2 }}\) can be represented in the integral form given in (24) we use the proof outlined in (Bochner 1937). According to Bernstein’s theorem (Widder 1946, Theorem 12.a) every completely monotone function can be written as a Laplace transform of some non-negative finite Borel measure μ. In Corollary 2 we have verified that \(\mathrm {e}^{-\frac {u^{\frac {p}{2}}}{2}}\) is a completely monotone function for p∈(0,2]. Therefore, according to Bernstein’s theorem, we can write \(\mathrm {e}^{-\frac {u^{\frac {p}{2}}}{2}}\) for p∈(0,2] as follows: for u>0
Substituting u=x2 into (78) completes the proof.
Appendix D: Proof of Proposition 5
To simplify the notation let \(r=\frac {2q}{p}\). To show that Xq=Vp,q·Xr, first observe that \(d \nu (t)=\frac {c_{q}}{c_{r}} \frac {1}{t^{\frac {1}{r}}} d\mu _{p}(t)\) is a probability measure where dμp(t) is the finite non-negative Borel measure defined in Theorem 1
where the equalities follow from: a) using the representation of \(\mathrm {e}^{-\frac {|x|^{p}}{ 2 }}\) in Corollary 3; and b) interchanging the order of integration which is justified by Tonelli’s theorem for positive functions.
The above implies that \(d \nu (t)=\frac {c_{q}}{c_{r}} \frac {1}{t^{\frac {1}{r}}} d\mu _{p}(t)\) is a probability measure on [0,∞). Moreover, for any measurable set \(\mathcal {S} \subset \mathbb {R}\) we have that
where the equalities follow from: a) the representation of \(\mathrm {e}^{-\frac {|x|^{p}}{ 2 }}\) in Theorem 1; b) the fact that \(d \nu (t)=\frac {c_{q}}{c_{r}} \frac {1}{t^{\frac {1}{r}}} d\mu _{p}(t)\) is a probability measure; c) because Xr is independent of t; and d) renaming \(V_{p,q}= \frac {1}{T^{\frac {1}{r} }}\). Therefore, it follows from (79) that Xq=dVp,q·Xr.
Next, we show that for p<2 the random variable Vp,q is unbounded. Any random variable Vp,q is unbounded if and only if
To show that Vp,q is unbounded observe that due to its non-negativity all the moments of Vp,q are given by
Moreover, by the assumption that p<2 we have that \(r=\frac {2q}{p} > q\), and by using Corollary 1 we have that for r>q
Therefore, Vp,q is an unbounded random variable for p<2. For p=2 we have that r=q and, hence, \(\mathbb {E}\left [ V_{p,q}^{k} \right ] =\frac { \mathbb {E}\left [|X_{q}|^{k}\right ]}{\mathbb {E}\left [|X_{r}|^{k}\right ]}= 1, \) for all k>0. Therefore, Vp,q=1 for p=2.
To find the pdf of Vp,q we use the Mellin transform approach by observing that
Therefore, by using Proposition 1 the Mellin transform of Vp,q is given by
Finally, the pdf of Vp,q is computed by the inverse Mellin transform of (80)
This concludes the proof.
Appendix E: Proof of Proposition 6
To simplify the notation let \(r=\frac {2q}{p}\). First, we show the power series representation of \(f_{V_{p,q}}(v)\) given in (28). Using the integral representation of \(f_{V_{p,q}}(v)\) in (26b) and the residue theorem we have that
where the sk are given by the poles of \(\Gamma \left (\frac {s +1}{q}\right)\) which occur at
Since the poles of \(\Gamma \left (\frac {s +1}{q}\right)\) are simple and \(\frac {1}{\Gamma \left (\frac {s+1}{r}\right)}\) is an entire function, the residue can be computed as follows:
where
Therefore, by putting (81), (82), and (83) together we arrive at
where
where the last step is due to the identity \( \Gamma (-x) \Gamma (x)=- \frac {\pi }{x \sin (\pi x)}\) and the identity Γ(x+1)=xΓ(x). The proof of this part is concluded by noting that a0=0.
To show the representation of \(f_{V_{p,q}}(v)\) in (30) we use the definition of the gamma function \(\Gamma (z)=\int _{0}^{\infty } x^{z-1} \mathrm {e}^{-x} dx\) as follows:
To validate the interchange of summation and integration in (84) observe that
where the (in)-equalities follow from: a) using the inequality |sin(x)|≤1; b) using the power series \(\mathrm {e}^{x}={\sum \nolimits }_{n=0}^{\infty } \frac {x^{n}}{n!}\); and c) using the fact that the integral converges since \( \frac {q}{r}-1= \frac {p}{2}-1 < 0\) and where we have used that \(p=\frac {2q}{r}\) and p<2 and, hence, \(2^{kq \left (\frac {1}{r} -\frac {1}{q} \right)} v^{kq} x^{\frac {kq}{r}} < x\) for large enough x.
The inequality in (85) together with Fubini’s theorem justifies the interchange of integration and summation in (84). Continuing with (84) we have
where the equalities follow from: a) using the identity \( \sin \left (\frac {\pi k q}{r} \right)= \frac {\mathrm {e}^{\frac {i \pi k q}{r}}-\mathrm {e}^{-\frac {i \pi k q}{r}} }{2 i} \); b) using the power series expansion \(\mathrm {e}^{x}={\sum \nolimits }_{n=0}^{\infty } \frac {x^{n}}{n!}\); and c) using the identity \(\frac { \mathrm {e}^{- \mathrm {e}^{-i \pi x} y}-\mathrm {e}^{- \mathrm {e}^{i \pi x} y} }{2i}=\sin \left (\sin \left (\pi x \right) y \right) \mathrm {e}^{- \cos \left (\pi x \right) y}\). Recalling that \(r = \frac {2 q}{p}\) we conclude the proof.
Appendix F: Proof of Proposition 9
The non-negativity of Up(x) follows from standard trigonometric arguments.
Next, it is not difficult to show that the derivative of Up(x) is given by
Observe that yp(x)≥0 for x∈(0,1) and all p∈(0,2]. The behavior of hp(x) is slightly more complicated and is given next.
Lemma 2
For p∈(0,1), hp(x)≥0 for all x∈(0,1), and for p∈(1,2]hp(x)≤0 for all x∈(0,1).
Proof
The proof of Lemma 2 is given in Appendix F.1. □
Lemma 2 together with the non-negativity of yp(x) shows that Up(x) is an increasing function for p∈(0,1) and a decreasing function for p∈(1,2].
Next, we show that the function \(g_{p}(x)=U_{p}(x) \mathrm {e}^{- |t|^{\frac {p}{p-1}} U_{p}(x) }\) has a single maximum by taking the derivative of gp(x):
Note that the location of the maximum of gp is given by
Since Up(x) is a strictly monotone function (either decreasing or increasing depending on p), the equation in (86) has only a single solution and therefore gp(x) has only one maximum. Moreover, from (86) the maximum is given by \(\max _{x \in [0,1]} g_{p}(x)= \frac {1}{\mathrm {e} |t|^{\frac {p}{p-1} }}. \) This concludes the proof.
F.1 Proof of Lemma 2
First observe that
Note that \(\frac {1}{1-p} \le 0\) for p>1 and \(\frac {1}{1-p}\ge 0\) for p<1. Therefore, we have to show that for all p∈(0,2)
The proof follows by looking at p∈(0,1) and p∈(1,2) separately.
For p∈(0,1) note that
where the inequalities follow from: a) using the fact that \( \cot \left (\frac {\pi p x}{2} \right) >0\) for all x∈(0,1) and all p∈(0,1); b) using the fact that (1−p)2≤1; and c) using the fact that 0<1−p<1 and the fact that \(\tan \left (\frac {\pi (1-p) x}{2} \right) \) is a monotonically increasing function for x∈(0,1).
For p∈(1,2) we look at two cases \(x \in (0, \frac {1}{2} ]\) and \(x \in \left (\frac {1}{2}, 1 \right)\). The reason we have to split the domain of x into two parts is because of the \(\cot \left (\frac {\pi p x}{2} \right)\). Note that \(\cot \left (\frac {\pi p x}{2} \right)\ge 0\) for all p∈(1,2) and all \(x \in (0, \frac {1}{2} ]\), but this is not true for the case of \(x \in \left (\frac {1}{2}, 1 \right)\).
Now, focusing first on the more involved case of \(x \in \left (\frac {1}{2}, 1\right)\) we have that
where the (in)-equalities follow from: a) using the fact that \(\tan \left (\frac {\pi x}{2} \right)>0\) and \( \tan \left (\frac {\pi (p-1) x}{2} \right)>0\), and using Cauchy-Schwarz inequality
b) using the identity \(\tan (\alpha +\beta)=\frac {\tan (\alpha)+\tan (\beta)}{1- \tan (\alpha)\tan (\beta)}\); and c) using the identity \(\tan (\alpha +\beta)=\frac {\tan (\alpha)+\tan (\beta)}{1- \tan (\alpha)\tan (\beta)}\).
Finally, we focus on the case of \(x \in \left (0, \frac {1}{2}\right)\),
where we have used the fact that \( \cot \left (\frac {\pi p x}{2} \right) > 0\) for \(x \in (0, \frac {1}{2})\) and p∈(1,2), and \( \tan \left (\frac {\pi x}{2} \right)>0\) for x∈(0,1), and \( \tan \left (\frac {\pi (p-1) x}{2} \right)>0\) for x∈(0,1) and p∈(1,2). This concludes the proof.
Appendix G: Proof of Proposition 10
To show that ϕp(t) can be represented by the power series we perform a ratio test and compute the radius of convergence as follows:
Now for p=1 the limit in (88) can be computed as follows:
Therefore, for p=1 we have that \(r=\frac {1}{2}\).
For p≠1 the limit in (88) can be computed using Stirling’s approximation
This concludes the proof.
Appendix H: Proof of Theorem 3
First, we show that for p>2 there is at least one zero. We use the approach of (Elkies et al. 1991). Towards a contradiction assume that ϕp(t)≥0 for all t≥0; then for t≥0
where the equalities follow from: a) using \((1-\cos (xt))^{2}= \frac {1}{2} \left (3-4 \cos (tx)+\cos (2tx)\right)\); and b) using the inverse Fourier transform. For small x we can write e−x=1−x+O(x2). Therefore,
As a result, for p>2 we reach a contradiction since 4−2p<0 for p>2. This concludes the proof for the case of p>2.
The fact that the number of zeros is countable follows from the fact that ϕp(t) is an analytic function according to Proposition 10. Recall that analytic functions on \(\mathbb {R}\) are either equal to a constant everywhere or have at most countably many zeros; the proof of this fact follows by using the identity theorem and the Bolzano-Weierstrass theorem.
For 0<p≤2, the result follows from Theorem 2 since \(\phi _{p}(t) = \mathbb {E} \left [ \mathrm {e}^{-\frac {t^{2}V_{G,p}^{2} }{2}}\right ]>0. \) This concludes the proof.
Appendix I: Proof of Proposition 11
Using the power series expansion of fG,p in (28) there exists a c>0 such that for v∈[0,c]
where \(B_{1}= \frac {\sqrt {\pi }}{\Gamma \left (\frac {1}{p} \right)} a_{1}\) with a1 defined as in (29). Therefore,
where we have used the integral \(\int _{0}^{c} v^{k} \mathrm {e}^{-\frac {v^{2} t^{2}}{2}} dv = \frac {2^{\frac {k-1}{2}}}{t^{k+1}} \gamma \left (\frac {k+1}{2}, \frac {c^{2}t^{2}}{2}\right)\). Next, using the expression in (91) and the limit \( {\lim }_{t \rightarrow \infty } \gamma \left (b, \frac {c^{2}t^{2}}{2}\right)=\Gamma \left (\frac {m+p+1}{2}\right)\) for any b,c>0
Next, we show that the second term in (92) is zero. To that end, observe that for any m+p>0 and any c>0 we have that \(t^{m+p+1}\mathrm {e}^{-\frac {v^{2} t^{2}}{2}} \le t^{m+p+1}\mathrm {e}^{-\frac {c^{2} t^{2}}{2}} \le B(c)<\infty \) for all t>0 where the constant B(c) is independent of t. Therefore,
where the finiteness of \(\mathbb {E}[ V_{G,p}^{m}]\) follows since \(\mathbb {E}[ V_{G,p}^{m}]= \frac {\mathbb {E}[|X_{p}|^{m}]}{\mathbb {E}[|X_{2}|^{m}]}\), and \(\mathbb {E}[|X_{p}|^{m}]\) and \(\mathbb {E}[|X_{2}|^{m}]\) are finite by Proposition 1. Therefore, by the dominated convergence theorem
The proof is concluded by noting that
Appendix J: Proof of Proposition 14
By symmetry of ϕp(t) the representation in (51) can be simplified to
Next, observe that σ2=(θ(0+)−θ(0−)) in the canonical representation in (51) is zero, since by Proposition 12, \(\sigma ^{2}= {\lim }_{t \to \infty } \frac {1}{t^{2}} \log (\phi _{p}(t)) =0.\) The parameter σ2 is sometimes referred to as the Gaussian component. Next, we show that θ(x) is an absolutely continuous distribution function by using the uniqueness of the Fourier transform. To that end, let
where g(t) is the cosine transform of the measure G(x).
We aim to show that θ(x) or equivalently G(x), in view of (94), is an absolutely continuous measure. A sufficient condition for G(x) to be absolutely continuous is the absolute integrability of g(t), that is \(\int _{-\infty }^{\infty } |g(t)| dt <\infty. \) Next, observe that g(t) is given by
Next, we give an upper bound on |g(t)| for large t. By the triangle inequality
where (95) follow from Proposition 11.
The bound in (95) implies that g(t) is absolutely integrable and G(x) and θ(x) have densities. Moreover, by the inversion formula for the cosine transform the density of G(x) and θ(x) are given by
Next, by using integration by parts we have for x≠0
where \( -\left (\log \phi _{p}(t) \right)^{\prime } \cos (tx) |_{0}^{\infty } =0\) follows from Proposition 11. For x=0 using (96) we have \(f_{G}(0)= - \frac {1}{\pi } \int _{0}^{\infty } \left (\log \phi _{p}(t) \right)^{\prime \prime } dt.\) This concludes the proof.
Appendix K: Proof of Theorem 6
Case of {(p,q):1<p=q}∖{(2,2)}
In this case, since p=q, we return to the proper definition of self-decomposability (Definition 8). From (Lukacs 1970, Theorem 5.11.1) we have that all distributions with self-decomposable characteristic functions are infinitely divisible. However, in Theorem 5 we have shown that GG distributions are not infinitely divisible for p∈(1,∞)∖{2}. Therefore, for p∈(1,∞)∖{2} the function ϕ(p,p,α)(t) is not a characteristic function.
Case of {(p,q):0≤p=q≤1}
In this case, since p=q, we return to the proper definition of self-decomposability (Definition 8). The proof of this case was outlined in (Bondesson 1992, p. 118) and it required the following definitions:
Definition 9
-
1
(Extended Generalized Gamma Convolution (EGGC) (Bondesson 1992, p.105).) An EGGC is a distribution on \(\mathbb {R}\) such that the bilateral Laplace transform \(\psi (s)=\mathbb {E}[\mathrm {e}^{sX}], \, s\in \mathbb {C}\), defined at least for Re(s)=0, has the form
$$ \psi(s)=\mathrm{e}^{bs+\frac{cs^{2}}{2} +\int \left(\log \left(\frac{t}{t-s} \right) -\frac{st}{1+t^{2}} \right) dU(t) }, $$(97)where \(b\in \mathbb {R}, c \ge 0\), and dU(t) is a non-negative measure on \(\mathbb {R} \setminus \{0 \}\) such that
$$ \int \frac{1}{1+t^{2}} dU(t)<\infty, \text{ and} \int_{|t|\le 1} | \log\left(t^{2}\right)| dU(t)<\infty. $$(98) -
2
(\(\mathcal {\beta }\)-Class (Bondesson 1992, p. 73).) A pdf f of a non-negative random variable belongs to the \(\mathcal {\beta }\)-Class if f can be written as follows:
$$ f(x)=C x^{\beta-1}\frac{h_{1}(x)}{h_{2}(x)}, \, x \ge 0, $$(99)where \(\beta \in \mathbb {R}, c \ge 0\) and, for j=1,2,
$$ h_{j}(x)=\mathrm{e}^{-b_{j} x+ \int \log\left(\frac{y+1}{y+x} \right) d \Gamma_{j}(y)}, \, x \ge 0, $$(100)where bj≥0 and dΓj(y) is a non-negative measure on (0,∞) satisfying
$$\int \frac{1}{1+y} d\Gamma_{j}(y)<\infty. $$ -
3
(Hyperbolic Completely Monotone (HCM) Function (Bondesson 1992, p. 55>).) A function f:(0,∞)↦(0,∞) is called HCM if, for each u>0, the function \(g(w)=\frac {f(uv)}{f \left (\frac {u}{v}\right)}\) is completely monotone as a function of w=v+v−1.
The following results are needed for our proof.
Theorem 7
(Properties of the EGGC, β-Class and HCM Functions.)
-
1
(Bondesson 1992, p. 107) An EGGC distribution is self-decomposable.
-
2
(Bondesson 1992, Theorem 7.3.3) Let X and Y be two independent random variables such that the distribution of X is EGGC and the distribution of Y is in the β-Class. If X is symmetric, then \(\sqrt {Y}X\) has an EGGC distribution.
-
3
(Bondesson 1992, Theorem 7.3.4) Let Y be a symmetric random variable on \(\mathbb {R}\) with a pdf fY. Then \(Y \stackrel {d}{=} \sqrt {V} Z_{2}\) is a Gaussian mixture such that the distribution of V is in the β-Class if and only if \(g(t)= f_{Y}(\sqrt {2t})\), t>0, is the Laplace transform of an HCM-function (or a degenerate function).
-
4
(Bosch and Simon 2016) Let fα:(0,∞)↦(0,∞) be a pdf of a positive α-stable distribution (i.e., the Laplace transform of fα is equal to \(\mathrm {e}^{-t^{\alpha }}\)). Then fα is HCM if and only if \( \alpha \in (0, \frac {1}{2})\).
First observe that the pdf of a GG random variable composed with \(\sqrt {2t}\) is given by \(f_{X_{p}}(\sqrt {2t})= c_{p} \mathrm {e}^{-2^{\frac {p}{2}-1}t^{\frac {p}{2}}}, \,t >0\), and is a Laplace transform, up to a normalization constant, of an α-stable positive random variable (see discussion in “Connection to stable distributions” section).
Next, let gp/2(x),x>0, denote the pdf of an α-stable distribution of order \(\frac {p}{2}\). Clearly, gp/2(x) is an inverse Laplace transform of \(f_{X_{p}}(\sqrt {2t})\) up to a normalization constant. Now by Theorem 7 Property 4) we have that gp/2(x) is an HCM function for all \(\frac {p}{2} \in (0, \frac {1}{2}]\). Therefore, \(f_{X_{p}}(\sqrt {2t})\) is a Laplace transform of an HCM function, and by Theorem 7 Property 3) \(f_{X_{p}}\) is a pdf of a Gaussian mixture \(X_{p} \stackrel {d}{=}\sqrt {V} X_{2}\) where the distribution of V is in the β-Class. By Theorem 7 Property 2) and Property 1) we have that for all \(\frac {p}{2} \in (0, \frac {1}{2}] X_{p}\) has an EGGC distribution and is self-decomposable.
Case of q>p>0
In this regime, we want to show that there exists no random variable \(\hat {X}_{\alpha }\) independent of \(Z_{p} \sim \mathcal {N}_{p}(0,1)\) such that \(\alpha X_{q}=\hat {X}_{\alpha }+Z_{p}\), where \(X_{q} \sim \mathcal {N}_{q}(0,1)\) for all α≥1. Note that Xq and Zp have symmetric distributions and finite moments, and thus if such an \(\hat {X}_{\alpha }\) exists it must also be symmetric with finite moments. Then for all k≥1
where the (in)-equalities follow from: a) Jensen’s inequality; and b) the independence of \(\hat {X}_{\alpha }\) and Zp, and that \(\mathbb {E}[\hat {X}_{\alpha }]=0\).
This implies that, in order for the inequality in (101) to hold we must have that
However, by Corollary 1 for p<q we have that \(\alpha \ge {\lim }_{k \to \infty } \left (\frac {\mathbb {E}[ |Z_{p}|^{k} ] }{\mathbb {E}[|X_{q}|^{k}] }\right)^{\frac {1}{k}} =\infty ;\) therefore, there exists no α≥1 that can satisfy (102) for all k≥1.
Case of p=2 and q<2
Note that in the case of p=2 and q<2 we want to show that there is no \(\hat {X}_{\alpha }\) such that the convolution leads to \( f_{X_{q}}(y) = c_{2} \mathbb {E} \left [ \mathrm {e}^{-\frac {\left (y-\hat {X}_{\alpha }\right)^{2}}{2}} \right ]\) where by definition \(f_{X_{q}}(y) = \frac {c_{q}}{\alpha } \mathrm {e}^{-\frac {|y|^{q}}{2 \alpha ^{q}}}\). Such an \(\hat {X}_{\alpha }\) does not exist since the convolution preserves analyticity. In other words, the convolution with an analytic pdf must result in an analytic pdf. Noting that \(f_{X_{q}}(y)\) is not analytic for q<2 (i.e., the derivative at zero is not defined) leads to the desired conclusion.
Case of p>2 and q≤2
Now for p>2 and q≤2 the function ϕ(q,p,α)(t) has a pole but no zeros by Theorem 3. Therefore, for the case of p>2 and q≤2 there exists a t0, namely the pole of ϕ(q,p,α)(t), such that ϕ(q,p,α)(t) is not continuous at t=t0. This violates the condition that the characteristic function is always a continuous function of t and, therefore, ϕ(q,p,α)(t) is not a characteristic function for all α≥1.
Case of p>q>2
For the case of p>q>2 the function \(\phi _{(q,p,\alpha)}(t)=\frac {\phi _{q}(\alpha t)}{\phi _{p}(t)}\) has both poles and zeros by Theorem 3. Moreover, let t1 be such that ϕp(t1)=0 and we can always choose an α such that ϕq(αt1)≠0 and ϕ(q,p,α)(t1)=∞. In other words, we choose an α such that the poles do not cancel the zeros. Therefore, there exists an α such that ϕ(q,p,α)(t) is not a continuous function of t and therefore is not a characteristic function. Finally, because the number of zeros is at most countable (see Theorem 3) the above argument holds for almost all α≥1.
Case of q<p<2
Finally, for q<p<2 the result follows from Proposition 12 where it is shown that \( {\lim }_{t \to \infty } \phi _{(q,p,\alpha)}(t)=\infty \), which violates the fact that the characteristic function is bounded. This concludes the proof.
Appendix L: Proof of Proposition 15
The magnitude of ϕlog(V)(t) can be approximated by using Stirling’s formula
Next, observe that
As a result, for p>q we have that |ϕlog(V)(t)| is not a bounded function and cannot be a characteristic function. For p<q, |ϕlog(V)(t)| is a bounded and integrable function. Therefore, ϕlog(V)(t) has a Fourier inverse given by
The proof is concluded by using the transformation \(f_{V}(v)= f_{\log (V)}(\log (v)) \frac {1}{v}\)
Notes
In other words, the set of α for which the statement does not hold has Lebesgue measure zero.
References
Abramowitz, M., Stegun, I. A.: Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables vol. 55. Courier Corporation, Chelmsford (1964).
Algazi, V. R., Lerner, R. M.: Binary detection in white non-Gaussian noise. M.I.T. Lincoln Lab. 18(Res. DS-2138), 241–250 (1964).
Arellano-Valle, R. B., Richter, W. -D.: On skewed continuous ℓ n,p-symmetric distributions. Chil. J. Stat. 3(2), 193–212 (2012).
Banerjee, S., Agrawal, M.: Underwater acoustic noise with generalized Gaussian statistics: Effects on error performance. In: Proceedings of OCEANS - Bergen, 2013 MTS/IEEE, pp. 1–8. IEEE, Bergen (2013).
Beaulieu, N. C., Young, D. J.: Designing time-hopping ultrawide bandwidth receivers for multiuser interference environments. Proc. IEEE. 97(2), 255–284 (2009).
Bernard, O., D’Hooge, J., Fribouler, D.: Statistical modeling of the radio-frequency signal in echocardiographic images based on generalized Gaussian distribution. In: Proceedings of the 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro, 2006, pp. 153–156. IEEE, Arlington (2006).
Bochner, S.: Stable laws of probability and completely monotone functions. Duke Math. J. 3(4), 726–728 (1937).
Bondesson, L.: Generalized gamma convolutions and related classes of distributions and densities. Lect. Notes Stat. 76 (1992).
Bosch, P., Simon, T.: A proof of Bondesson’s conjecture on stable densities. Ark Matematik. 54(1), 31–38 (2016).
Cover, T., Thomas, J.: Elements of Information Theory: Second Edition. Wiley, Hoboken (2006).
De Simoni, S.: Su una estensione dello schema delle curve normali di ordine r alle variabili doppie. Statistica. 37, 447–474 (1968).
de Wouwer, G. V., Scheunders, P., Dyck, D. V.: Statistical texture characterization from discrete wavelet representations. IEEE Trans. Image Process. 8(4), 592–598 (1999).
Do, M. N., Vetterli, M.: Wavelet-based texture retrieval using generalized Gaussian density and Kullback-Leibler distance. IEEE Trans. Image Process. 11(2), 146–158 (2002).
Dytso, A., Bustin, R., Poor, H. V., Shamai (Shitz), S.: A view of information-estimation relations in Gaussian networks. Entropy. 19(8), 409 (2017).
Dytso, A., Bustin, R., Poor, H. V., Shamai (Shitz), S.: On additive channels with generalized Gaussian noise. In: Proceedings of the IEEE International Symposium on Information Theory, pp. 426–430. IEEE, Aachen (2017).
Dytso, A., Bustin, R., Tuninetti, D., Devroye, N., Poor, H. V., Shitz, S. S.: On the minimum mean p-th error in Gaussian noise channels and its applications. IEEE Trans. Inf. Theory. 64(3), 2012–2037 (2018).
Elkies, N., Odlyzko, A., Rush, J.: On the packing densities of superballs and other bodies. Invent. Math. 105(1), 613–639 (1991).
Eskenazis, A., Nayar, P., Tkocz, T.: Gaussian mixture entropy and geometric inequalities (2016). Preprint available at https://arxiv.org/abs/1611.04921.
Fahs, J., Abou-Faycal, I.: On properties of the support of capacity-achieving distributions for additive noise channel models with input cost constraints. IEEE Trans. Inf. Theory. 64(2), 1178–1198 (2018).
Goodman, I. R., Kotz, S.: Multivariate θ-generalized normal distributions. J. Multivar. Anal. 3(2), 204–219 (1973).
Gauss, C. F.: Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientium vol. 7. Perthes et Besser, Paris (1809).
Gonzalez-Jimenez, D., Perez-Gonzalez, F., Comesana-Alfaro, P., Perez-Freire, L., Alba-Castro, J. L.: Modeling Gabor coefficients via generalized Gaussian distributions for face recognition. In: Proceedings of the IEEE International Conference on Image Processing, vol. 4, pp. 485–488. IEEE, San Antonio (2007).
Gupta, A. K., Nagar, D. K.: Matrix Variate Distributions. Chapman and Hall/CRC, London (2018).
Hoffman-Jørgensen, J.: Probability with a View Towards Statistics vol. 2. Routledge, Abingdon (2017).
Levy, H.: Stochastic dominance and expected utility: survey and analysis. Manag. Sci. 38(4), 555–593 (1992).
Lévy, P.: Calcul des Probabilités. Gauthier-Villars, Paris, France (1925).
Lin, G. D., Huang, J. S.: The cube of a logistic distribution is indeterminate. Aust. J. Stat. 39(3), 247–252 (1997).
Lukacs, E.: Characteristic Functions. Griffin, Londong (1970).
Lutwak, E., Yang, D., Zhang, G.: Moment-entropy inequalities for a random vector. IEEE Trans. Inf. Theory. 53(4), 1603–1607 (2007).
Mallat, S. G.: A theory for multiresolution signal decomposition: the wavelet representation. IEEE Tran. Pattern Anal. Mach. Intell. 11(7), 674–693 (1989).
McLachlan, G., Peel, D.: Finite Mixture Models. Wiley, Hoboken (2004).
Miller, J., Thomas, J. B.: Detectors for discrete-time signals in non-Gaussian noise. IEEE Trans. Inf. Theory. 18(2), 241–250 (1972).
Mohamed, O. M. M., Jaidane-Saidane, M., Souissi, J.: Modeling of the load duration curve using the asymmetric generalized Gaussian distribution: case of the Tunisian power system. In: Proceedings of the 10th International Conference on Probabilistic Methods Applied to Power Systems, pp. 1–6. IEEE, Rincon (2008).
Moulin, P., Liu, J.: Analysis of multiresolution image denoising schemes using generalized Gaussian and complexity priors. IEEE Trans. Inf. Theory. 45(3), 909–919 (1999).
Nadarajah, S.: A generalized normal distribution. J. Appl. Stat. 32(7), 685–694 (2005).
Nielsen, P. A., B.Thomas, J.: Signal detection in Arctic under-ice noise. In: Proceedings of the 25th Annual Allerton Conference on Communication, Control, and Computing, pp. 172–177. IEEE, Monticello (1987).
Nielsen, F., Nock, R.: Maxent upper bounds for the differential entropy of univariate continuous distributions. IEEE Signal Process. Lett. 24(4), 402–406 (2017).
Olver, F.: Uniform, exponentially improved, asymptotic expansions for the generalized exponential integral. SIAM J. Math. Anal. 22(5), 1460–1474 (1991).
Ozarow, L. H., Wyner, A. D.: On the capacity of the Gaussian channel with a finite number of input levels. IEEE Trans. Inf. Theory. 36(6), 1426–1428 (1990).
Pogány, T. K., Nadarajah, S.: On the characteristic function of the generalized normal distribution. C. R. Math. 348(3), 203–206 (2010).
Poor, H. V., Thomas, J. B.: Locally optimum detection of discrete-time stochastic signals in non-Gaussian noise. J. Acoust. Soc. Am. 63(1), 75–80 (1978).
Poularikas, A. D.: Handbook of Formulas and Tables for Signal Processing. CRC Press, Boca Raton (1998).
Richter, W. -D.: Generalized spherical and simplicial coordinates. J. Math. Anal. Appl. 336(2), 1187–1202 (2007).
Richter, W.-D.: Geometric disintegration and star-shaped distributions. J. Stat. Distrib. Appl. 1(1), 20 (2014).
Richter, W.-D.: Exact inference on scaling parameters in norm and antinorm contoured sample distributions. J. Stat. Distrib. Appl. 3(1), 8 (2016).
Schilling, R. L., Song, R., Vondracek, Z.: Bernstein Functions: Theory and Applications vol. 37. Walter de Gruyter, Berlin, Germany (2012).
Sharifi, K., Leon-Garcia, A.: Estimation of shape parameter for generalized Gaussian distributions in subband decompositions of video. IEEE Trans. Circ. Syst. Video Technol. 5(1), 52–56 (1995).
Soury, H., Yilmaz, F., Alouini, M. -S.: Average bit error probability of binary coherent signaling over generalized fading channels subject to additive generalized Gaussian noise. IEEE Commun. Lett. 16(6), 785–788 (2012).
Soury, H., Alouini, M. S.: New results on the sum of two generalized Gaussian random variables. In: Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing, pp. 1017–1021. IEEE, Orlando (2015).
Subbotin, M.: On the law of frequency of error. Matematicheskii Sb. 31, 296–301 (1923).
Stewart, J.: Positive definite functions and generalizations, an historical survey. Rocky Mt. J. Math. 6(3), 409–434 (1976).
Stoyanov, J.: Krein condition in probabilistic moment problems. Bernoulli Journal. 6(5), 939–949 (2000).
Ushakov, N. G.: Selected Topics in Characteristic Functions. Walter de Gruyter, Berlin, Germany (1999).
van Harn, K., Steutel, F.: Infinite Divisibility of Probability Distributions on the Real Line. Taylor & Francis, New York (2003).
Varanasi, M. K., Aazhang, B.: Parametric generalized Gaussian density estimation. J. Acoust. Soc. Am. 86(4), 1404–1415 (1989).
Vasudevay, R., Kumari, J. V.: On general error distributions. ProbStat Forum. 06, 89–95 (2013).
Viswanathan, R., Ansari, A.: Distributed detection of a signal in generalized Gaussian noise. IEEE Trans. Acoust. Speech, Signal Process. 37(5), 775–778 (1989).
Westerink, P. H., Biemond, J., Boekee, D. E.: Subband coding of color images. In: Subband Image Coding, pp. 193–227. Springer, Boston (1991).
Widder, D. V.: The Laplace Transform. 1946. Princeton University Press, Princeton (1946).
Zolotarev, V. M.: One-dimensional Stable Distributions vol. 65. American Mathematical Society, Providence (1986).
Acknowledgements
The authors would like to thank Professor Alexander Lindner from the Ulm University for providing references (Bondesson 1992) and (Bosch and Simon 2016), which immediately lead to the conclusion that the GG distributions in p∈(0,1] are self-decomposable.
Funding
The work of A. Dytso and H.V. Poor was supported by the U.S. National Science Foundation under Grant CNS-1702808. The work of S. Shamai and R. Bustin was supported by the European Union’s Horizon 2020 Research and Innovation Programme Grant 694630.
Availability of data and materials
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dytso, A., Bustin, R., Poor, H. et al. Analytical properties of generalized Gaussian distributions. J Stat Distrib App 5, 6 (2018). https://doi.org/10.1186/s40488-018-0088-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40488-018-0088-5